

In the statement of our confidence interval it is important to indicate the level of confidence. This can be expressed as either Estimate ± Margin of Error or as Estimate - Margin of Error to Estimate + Margin of Error.
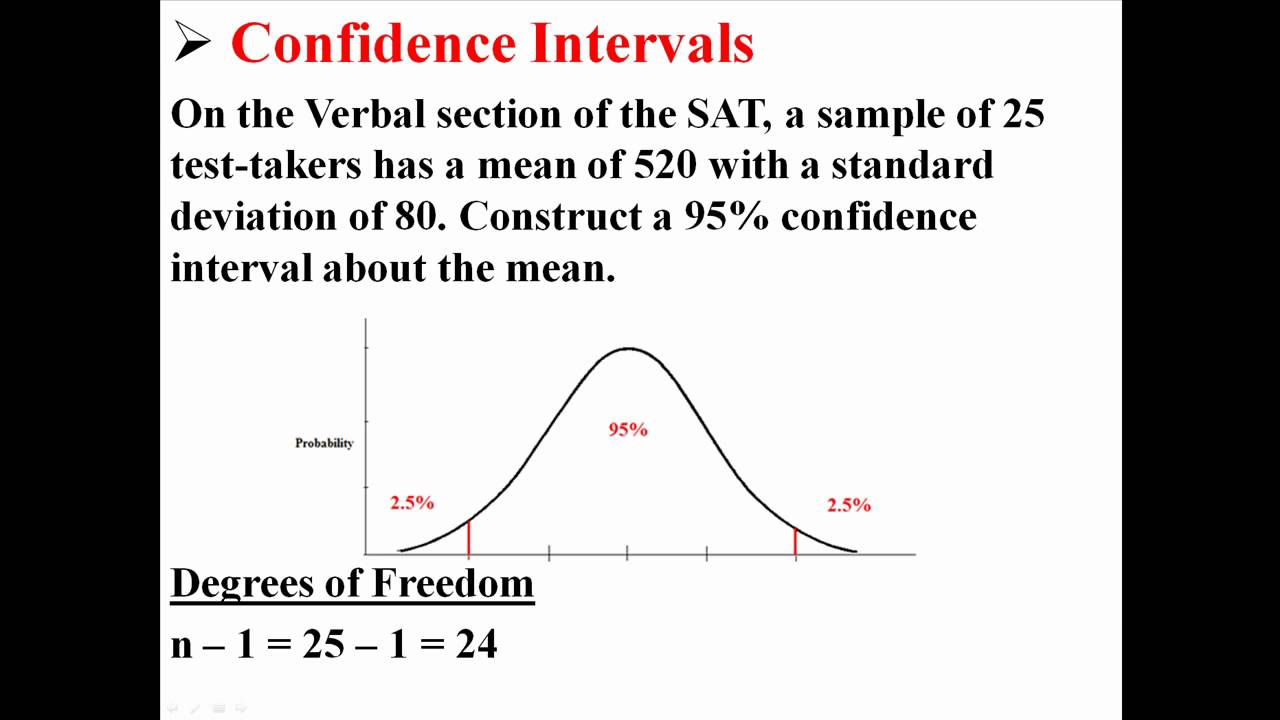
Conclude: Finish by putting together the estimate and margin of error.This confidence interval tells us how confident or certain we are that the true population mean ( µ) falls within a given range. The SE allows us to calculate a confidence interval around a particular sample mean. Margin of Error: Calculate the margin of error t * s /√ n, where n is the size of the simple random sample that we formed and s is the sample standard deviation, which we obtain from our statistical sample. Roughly, the standard error (SE) is to a distribution of many sample means as the standard deviation (sd) is to a distribution of scores in one sample.The way we would interpret a confidence interval is as follows: There is a 95 chance that the confidence interval of 5.064, 8.812 contains the true population. Confidence Interval for a Standard Deviation: Interpretation. The number of degrees of freedom is one less than the number of individuals in our sample. Note: You can also find these confidence intervals by using the Confidence Interval for a Standard Deviation Calculator. If we use a table, we will need to know the number of degrees of freedom. These values are found by consulting a table of t-scores or by using the software. It also provides an error bar diagram and the calculation steps. This function calculates the standard error of an effect size provided the exact(p)-value and (continuous) effect size according to the formulaby Altman and Bland (2011). Critical Value: We obtain the critical value t * that correspond with our confidence level. Calculator to compute the confidence interval or margin of error of a sample based on the desired confidence level.You are going to choose 95 in this example.

4) Choose the desired confidence level: The most common confidence levels are 90, 95, and 99. Our standard deviation value is approximately 0,5. The result of this calculation will be 0,5011. Sometimes we can suppose that our sample is a simple random sample, even if it does not meet the strict definition. It might sound complicated but you can use a calculator for this step. This involves forming a simple random sample from our population. Calculate Estimate: We estimate our population parameter, in this case, the population mean, by use of a statistic, in this case, the sample mean.We can relax the assumption that we have a normal distribution as long as our sample is large enough and has no outliers or extreme skewness. We assume that the value of the population standard deviation, denoted by the Greek letter sigma σ, is unknown and that we are working with a normal distribution. Check Conditions: Begin by making sure that the conditions for our confidence interval have been met. the procedures above it follows that for a test score of, say standard score 106, the confidence intervals will be: Standard Score Test 1 Reliability 0.75 SEm 7.5 Test 2 Reliability 0.


 0 kommentar(er)
0 kommentar(er)
